3.7章　算数：てこの問題

ここはタール村にある、唯一の図書館。建物には良い光が入り、周りは自然に囲まれている。

その図書館には、優しそうな館長と、肝っ玉母ちゃんのような司書のゴシカがいつもいる。近くの学校からは物静かなスイスイという女の子がよく来ていた。

今日はそんな図書館にある、一冊の本を読んでみよう。

問題

以下のような重い石をてこで持ち上げるとします。

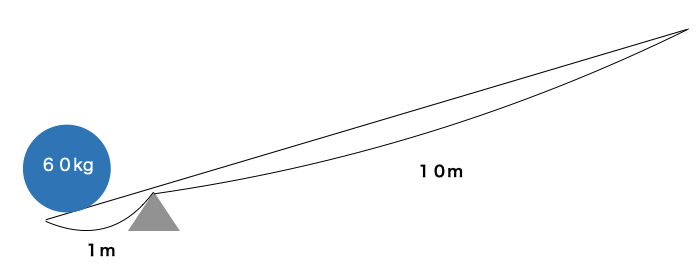
この時、何kgの重さで右側に力を込めれば、持ち上げることができるでしょうか。

腑に落ちないスイスイ

タール村の図書館で借りた算数の問題集の、このてこの問題を見て、スイスイは辟易してしまった。

この問題の答えは６kgである。そもそもてこには力点、支点、作用点の三つのポイントがある。先ほどの問題に関してはこうなる。

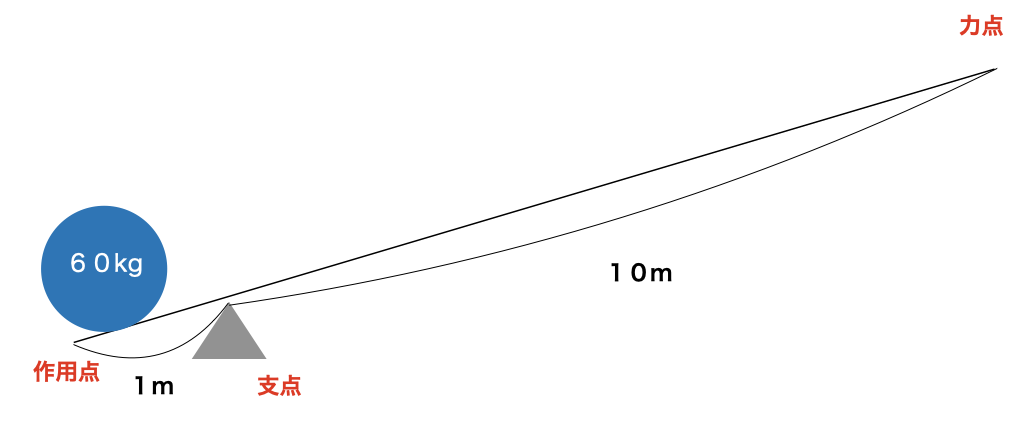
棒を支える点が支点、力を込める点が力点、動かす対象の石があるところが作用点である。

そして公式として、支点を境にして、右と左の力が同じになるというものがある。かつそのそれぞれの力は、支点からの距離×重さで導くことができる。

左側で言えば、１m×６０kg＝６０。

そして右側は１０m×○。右と左の力は同じとなるため、答えは左側と同じく６０。１０m×○＝６０となり、○に入るのは６kgとなる。

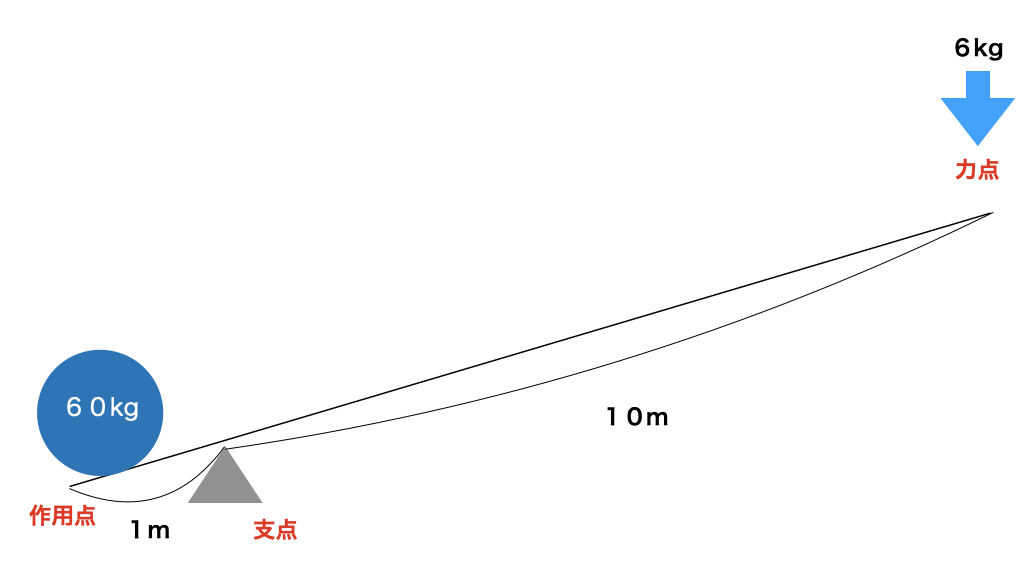
答えは導き出せるのだが、スイスイは何か腑に落ちないものを感じていた。なぜてこを使うと、小さい力で、重いものを持ち上げることができるのだろう。

この公式にはおまけがあって、小さい力で重いものを持ち上げるのには二つの方法がある。

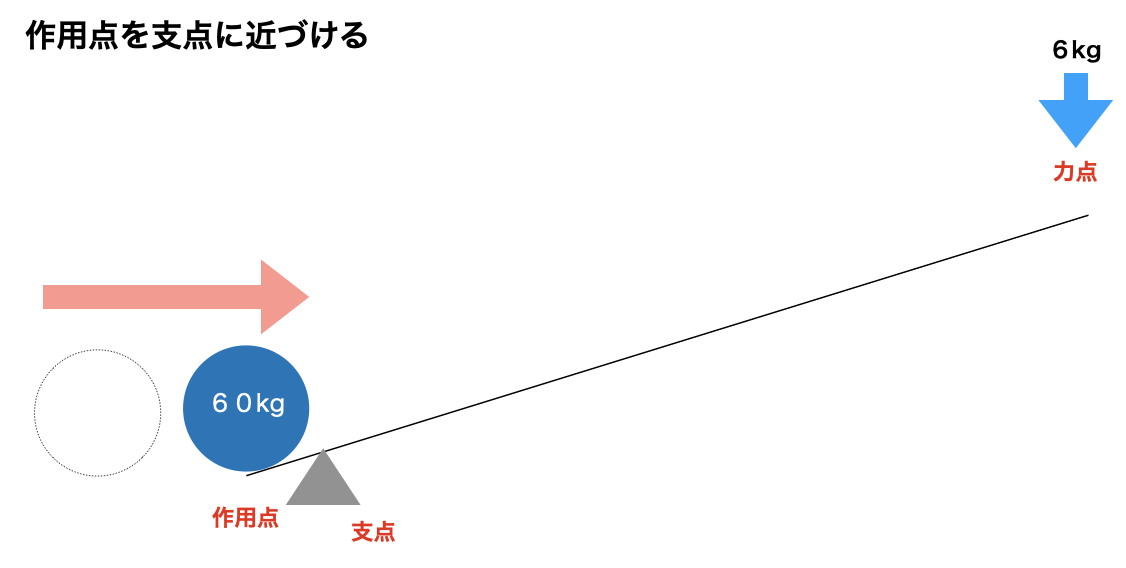
一つ目は作用点を支点に近づけること、もう一つは、力点を支点から遠ざけることだ。

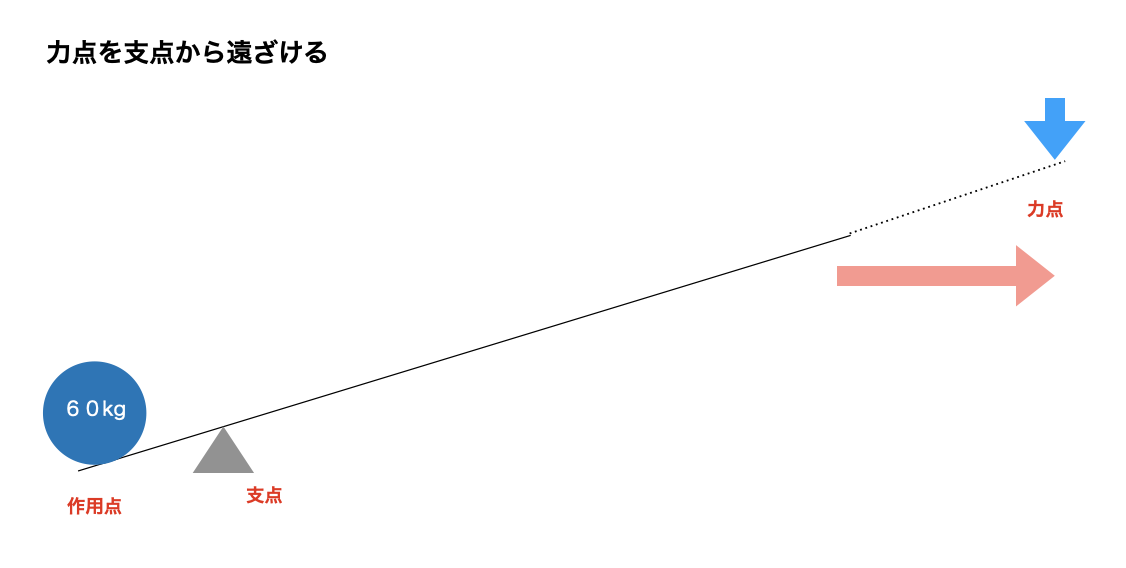
なぜこのようなことが起きるのだろうか。

そもそもなぜ距離を変えたりすることで、発生する力が変わってくるのだろう。

わけがわからないという様子で困っていたスイスイを見て、館長が近づいてきた。

てこは三角形で考える

「スイスイさん、問題が難しくて、お困りのようですね」

そう言って、優しそうに笑って、館長はスイスイに話しかけた。

コクリとうなづき、スイスイは館長に相談した。

「館長、てこの問題なんだけど、私全然わからないの。
　てこって本当に不思議。どうして支点からの距離を変えると、込める力が変わるんだろう。
　だって重い石は重い石だし、私の力だって、急に変わったりしない。でも距離を変えるとなぜ込める力の量が変わるのか、なんだか腑に落ちないの」

一気にまくしたてたスイスイの後ろから、司書のゴシカも会話に参加してきた。

「あー、なんか私も子どもの時にやったなー、この支点とか作用点とかのやつ。あと滑車の問題ね。今やってもできる気がしないわ」

そういってカラカラとゴシカは笑った。

気を取り直して館長はスイスイに話した。

「スイスイさんは、どうしててこが、作用点や力点の位置を変えるだけで、込める力の量が変わる点に、納得がいっていないという感じですか」

「そう、なんで距離によって力が変わるのかがわからないの」

「であれば、こういうふうに考えてみてはいかがですか」

そう言って、館長は図を描いた。

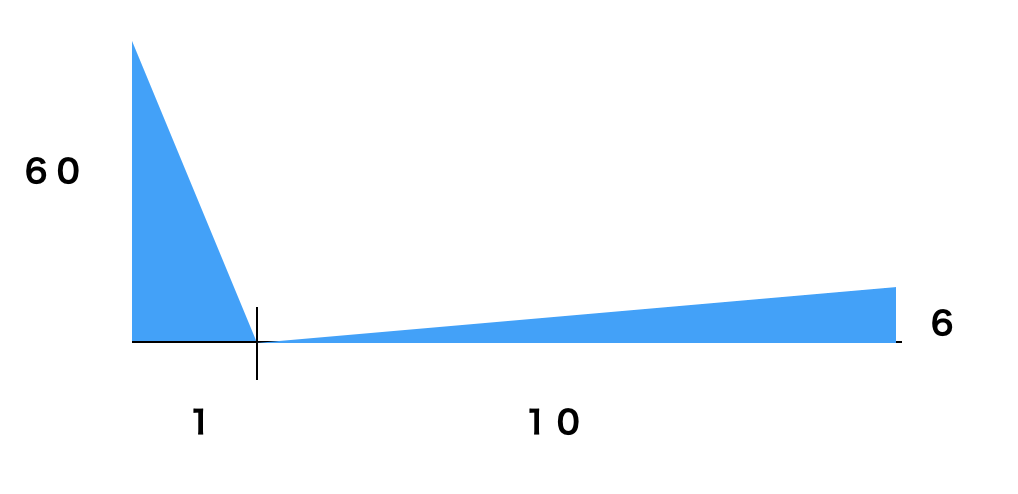
「先ほどの問題だと、左、作用点の方ですね、それが６０kgの石で、支点から１m。そして右が支点から力点までで１０m、そして込める力が６kgでした。
　仮に力を縦軸、支点からの距離を横軸とした時、このような三角形が出来上がります。
　さてスイスイさん、この時左の三角形の面積はなんですか」

質問されたスイスイはすぐに答えた。

「６０×１÷２で、３０です」

「正解です、では右は？」

「こっちは６×１０÷２で、こっちも３０です」

「そうなんです、公式で、支点を境にして右と左にかかる力は等しくなるというのがありますが、重さという目には見えないものを算数では縦軸として見ると、三角形の計算と似ていますので、イメージがつきやすいと思います」

ゴシカも感心して言った。

「なるほどね〜、確かに面積が変わらないのであれば、力点から支点までの距離を伸ばせば伸ばすほど、力点で必要な重さは減るわね」

「どういうこと、ゴシカさん」

少し話についていけていなそうなスイスイはゴシカに質問した。

「あ、ごめんごめん、つまりね、力点から支点までの距離を仮に１０mから２０mにするじゃない？
　でも面積が変わらず３０だったとする。式で言えば、２０×○÷２＝３０で、○に入るのは６０÷２０で３になるわ。
　つまり距離を２０mに伸ばせば、６kgからさらに３kgで力が済むことになるのよ」

「すごい、さらに力がいらなくなるんだ」

「そうね、あとは作用点を支点に近づけるってことだけど。
　左側が６０kgの石に支点からの距離が１mなのよね。この時の力は１m×６０kgで６０だわね。
　でも支点から作用点までの距離を短くしてみる。例えば0.５m。そうすると、0.５×６０kgで、３０になるわ。
　こうなると、右側は１０m×○＝３０になるので、○は３。つまり３kgで持ち上げられることになったわ！」

ゴシカは少し興奮気味にスイスイに話した。スイスイも話を理解したようだ。

「なるほどね〜、重さを縦の長さみたいに考えて、面積のように見ると、わかりやすいね」

館長はうなづいた。

「そうですね、スイスイさん。今回は三角形で面積を考えましたが、三角形だと÷２をいちいちしなくてはいけないので、ちょっと面倒ですね。まあ結局左辺も右辺も÷２をするのですから、いちいち÷２をする必要はありません。今回はイメージを掴むためにやりましたけどもね」

館長は満足そうにもう一度うなづいた。

「でもこうなると、本当にてこは便利よね。距離を伸ばせば伸ばすほど大きな力が出るなんて。なんか無敵みたい」

ゴシカが言った発言が、スイスイも気になっていた。なんだかてこは無敵のような感じがするのだ。欠点がない最強の手段。でもそんなことが本当にあるのだろうか。

「いい着眼点だと思いますよ、ゴシカさん。そう、実はてこは万能ではない、ある重大な弱点があるのです」

「えっ、それってなんなの！」

それが聞きたかったという様子で、食い入るようにスイスイが質問してきた。

館長はうなづき、こう発言した。

「それはものすごい長い距離が必要ということです」

てこの弱点

「距離、、、確かに込める力を減らすには、力点を支点から遠ざける必要があったわね」

ゴシカは独り言のように呟いた。

「そうなんです、てこは込める力を減らしたかったら、それと反比例して支点からの距離が伸びるのです。
　こんな例で考えてみましょう。重たい荷馬車、そうですね、思い切って１０００kgあるとしましょう。まあ１トンですね。これの滑車のところにものが挟まってしまい、それを取るために荷馬車をぐいっと持ち上げなければならないですと。その時にてこを使うことになりました。
　荷馬車は１０００kg、ここが作用点ですね。そして作用点から支点までの距離は１m。てこの反対側に人がぐいと持ち上げる。その人が込められる力が体重と同じ５０kgとしましょう。
　さて、スイスイさん。この時支点からその人までの距離、つまり力点までの距離なのですが、何m必要だと思いますか」

聞かれたスイスイは暗算で答えた。

「つまり荷馬車の方が１m×１０００kgで１０００だよね。
　で人の方が○m×５０で、これが同じく１０００になるんだから、１０００÷５０で２０。
　えっ、２０mも必要なの！」

驚いた様子でスイスイは言った。

「そうなんです、１トンのものを持ち上げることができますが、それには２０mも離れたところから力を込めなければならないんです。ちょっと面倒というか、そんな棒を用意できるかもわかりませんし、ちょっと非現実的ですよね」

ゴシカも発言した。

「うーん、そうねえ、ちょっと長すぎるわね。結局、何かを得るためには、何かを捨てなきゃいけないのかしらね」

メリットとデメリットは表裏一体

館長は、人差し指を立て、「その通り」と言いたげに、ゴシカとスイスイに話した。

「私が最も伝えたかった点はそこです。力を使わなくて良いというメリットを享受すると、その代わりに距離を稼がなくてはいけないというデメリットが発生するということなんです。
　この世には万能のツールなんて存在しないのだと思います。その時と場合に応じ、面積のような有限のリソースをうまく縦軸と横軸の長さを変えて対応して行く。そういったことが重要だと思うのです」

スイスイは加えてこう言った。

「なんか頑張る時と似ている。例えば頑張って勉強をすると、確かにテストの点数は良くなるかもしれないけど、すっごく疲れちゃうの。ずうっと頑張るなんてできないと思う。
　何かを頑張れば、その分どこかで休まなきゃいけない。そういうことなのかなあ」

そう言ったスイスイにゴシカは答えた。

「そうね、スイスイちゃん。ずっと頑張るなんて無理だよね。やれる量は変わらないんだから、どこかで頑張ったら、どこかで同じくらい休まないとね」

館長もそれについて同意だった。

とかく、最近は頑張ることが奨励され、休むことが忌み嫌われる傾向がある。しかし頑張ることと休むことは表裏一体。てこの重さと距離と同じだ。計算の結果得られるものが同じであれば、どちらかを増やせば、どちらかを減らす必要がある。増やし続けることはできないし、減らし続けることもできない。

館長は今週のおすすめコーナーに、この算数の本を置いた。ちょうど学校も夏休みで子どもたちも暇だろう。算数の問題なんて嫌だろうが、館長はてこの問題を含んだこの問題集を、おすすめしたい気持ちを止められなかった。

以上