(125) なぜA4用紙を折っていっても、縦横比率はずっと変わらないのか
まず、紙のサイズの話
ぼくは最近、写真を大きいサイズに印刷し、額縁に入れて、家族の許可をもらって、家に飾るのにハマっている。
その際、用紙のサイズには恐ろしくたくさんの種類があるのに驚き、辟易した。
ぼくらに一番身近なサイズは、おそらくコピー用紙でも使われるA4用紙だろう。
A4用紙は、210mm×297mm。長い長辺が、30cm物差しぐらいの大きさだ。
それとは違い、B4サイズというのもある。B版はA版よりも一回り大きいのだが、暗記だと、少し経つと、AとB、どちらが大きいか忘れてくる。
まず理解しなければいけないのが、A版は最大どこまでのサイズがあるかということだ。
A版はA0サイズまである。これが大元のサイズで、それを2分割すると、A1。さらに2分割でA2サイズとなる。
そしてA0サイズとは、面積が1m2(1平方メートル)である。そのため、A 0サイズは841mm×1189mmとなる。これをかけ算すると、約1,000mm2で、1m2となる。
そしてB版だが、そのA版を1.5倍にしたものである。そのため面積は1.5m2となる。だから一回り大きいのだ。B0サイズは1030mm × 1456mmで、約1500mm2であり、1.5m2となる。
どのようにサイズアップ、サイズダウンするかという点は、例えば、なじみのある、A3サイズとA4サイズを例に取ってみると、
A4は先ほども書いたが、210×297である。これの短辺を2倍する、そうすると、420×297になる。要は半分ずつ折っているのだが、折った辺を2倍してやれば、前のサイズに戻るというわけだ。
また、A4からA5であれば、210×297から、長辺を2で割る、すると、297÷2=148.5。148.5×210が、A5サイズとなる。
あと、写真で言うと、よく写真をプリントする場合に使われる、L版と、それの倍の長さの2L版。
また、8つ切り、6つ切り、4つ切りなど、今度は画用紙の全紙と呼ばれる、A版でいうA0サイズみたいなものから、8等分、6等分、4等分して作られるサイズもある。
ぼくは最近この4つ切りで、さらに横に伸ばした、四つ切りワイドの形で写真を印刷したのだが、4つ切りとは、A4サイズの長辺はそのままもう少し縦が長くなるので、ちょっと正方形に近くなるイメージだ。無論、それより6つ切りが、さらに8つ切りの方が小さくなってくる。だが、この長さも一律ではない。なぜなら元の全紙の大きさが、色々と種類があるからだ。大きさがまちまちなので、それを4つ切りしたものも、当然大きさが変わってくる。これは元の紙の大きさがどのくらいかを確認した方がよく、4つ切りだからこの大きさとは、考えない方がいいだろう。
ではなぜ紙を折っても、比率が変わらないのか
ここからが本題なのだが、A版もB版も縦と横の比率は、√2:1となっている。√2とは、一夜一夜に人見頃なので、1.414くらい。つまり、1.414:1くらいの比率となっている。
これが不思議なもので、これを長辺で2等分してみる。例えば、A4サイズを2等分してA5サイズにするイメージだ。このとき、1より大きい√2の方を長辺として2等分するので、√2/2となる。
そうすると2等分してできたその紙の比率は、1:√2/2となる。じつはこれ、√2:1なのだ。
計算は下記のようになる。
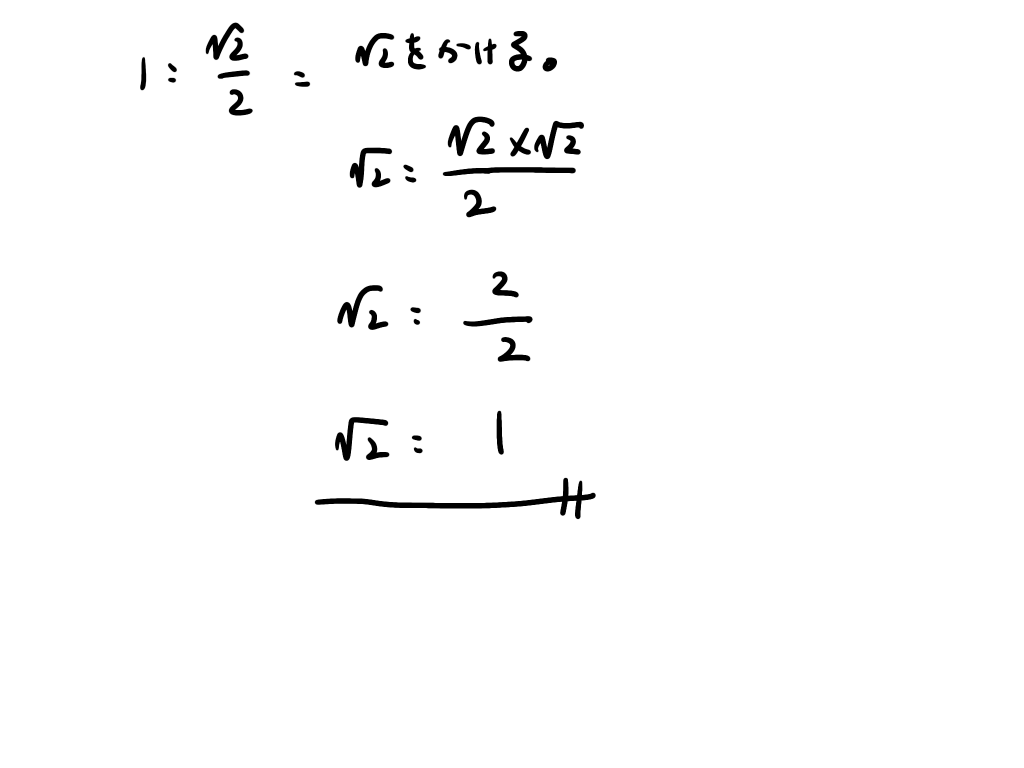
つまりこれの差すところは、折っても、縦横比の比率は変わってないということだ。図示すると以下のようになる。

これのおかげで、A0の紙を、余すことなく使えることができる。これも全て、比率を√2:1にしたおかげである。
しかしよくよく考えるとおかしくないかと思う。なぜこの比率の時だけ何度等分していっても、同じ比率になるのか。
不思議だと思うのであれば、例えば長細い紙を用意し、2等分に折ってみてほしい。するとどうだろう。その等分された紙は、最初の紙の比率と違うだろう。
なぜ√2:1の時だけ、このような事態、つまりこの比率がキープされることになるのだろうか。
これを解くためには、まず√2から離れなければならない。それと同じく、2等分するということからも離れなければならない。それぞれをXと置き換える。そして、この現象をおそらく数学的にいうと、以下の定義になるのだと思う。
X>1の場合、√X:1の長方形があったとする。これをX等分で折り曲げても、比率は変わらず√X:1となる。これを証明すると以下となる。

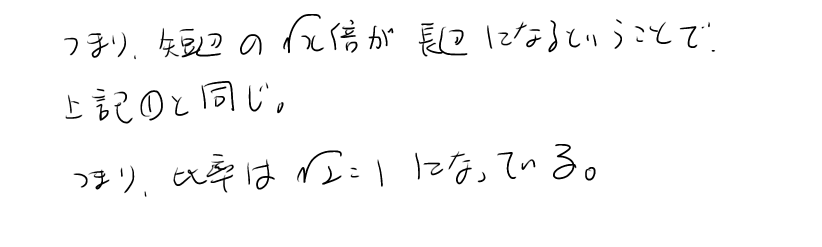
一応証明はできたと思うのだが、なんだか釈然とこない。そうなんだ、ふぅんでこれだと終わってしまう。これの一番のミソは、○等分するの○と、√○の○がイコールであるということだ。つまり、もし3等分するのだったら、√3:1の紙にしてあげれば、3等分された紙の寸法は、元の紙と一緒ということになる。
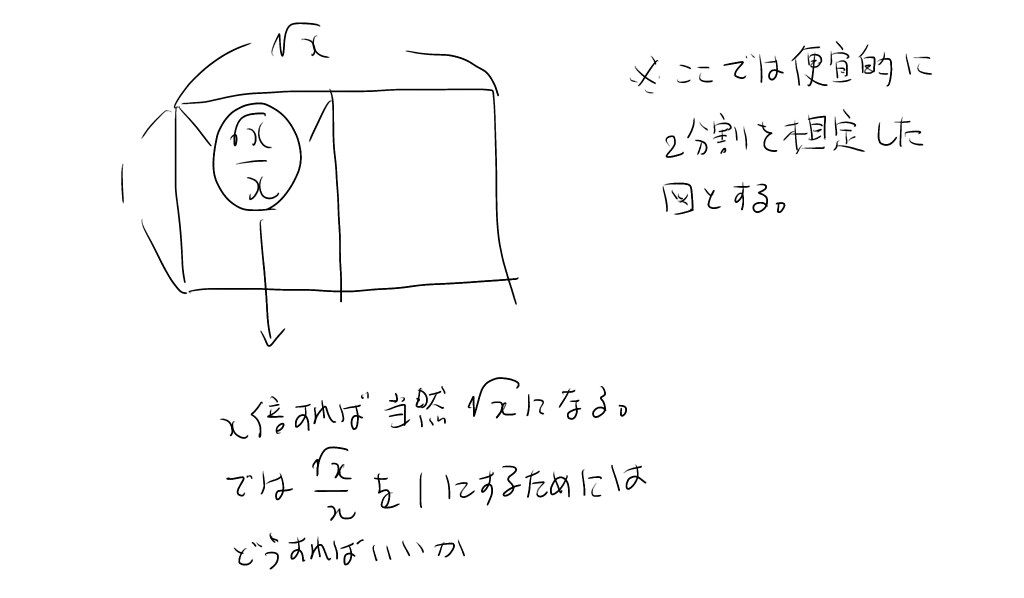
そして今度は一旦紙を折るという概念から一旦離れ、数学式としてこの現象を見てみる。
√XをXで割れば、√X /Xとなる。当然これにX倍すれば、元の√Xに戻る。
そして√X/Xを1にするためにはどうすればいいかを考える。
すると、以下のようなことが言える。

そして、このX/√Xが大事なのである。
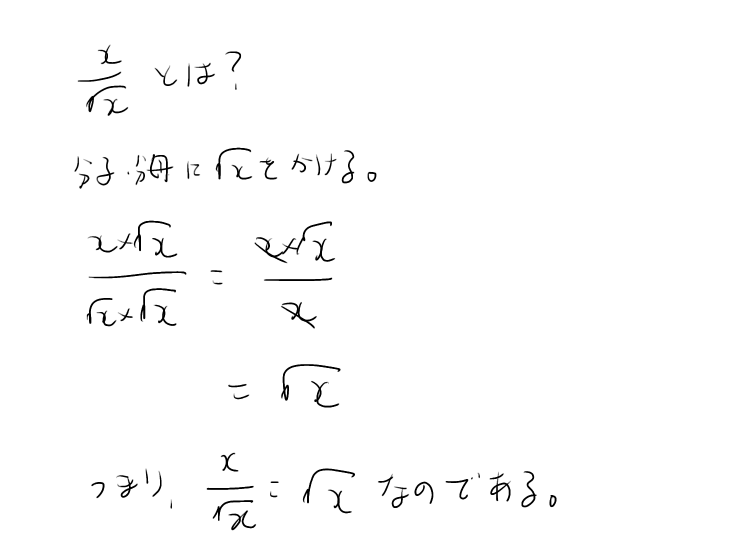
X/√Xが、そもそも√Xだったとは、なかなか連想しにくい。
そしてここからわかることは、√X/Xに、√Xをかけると1になるということなのである。
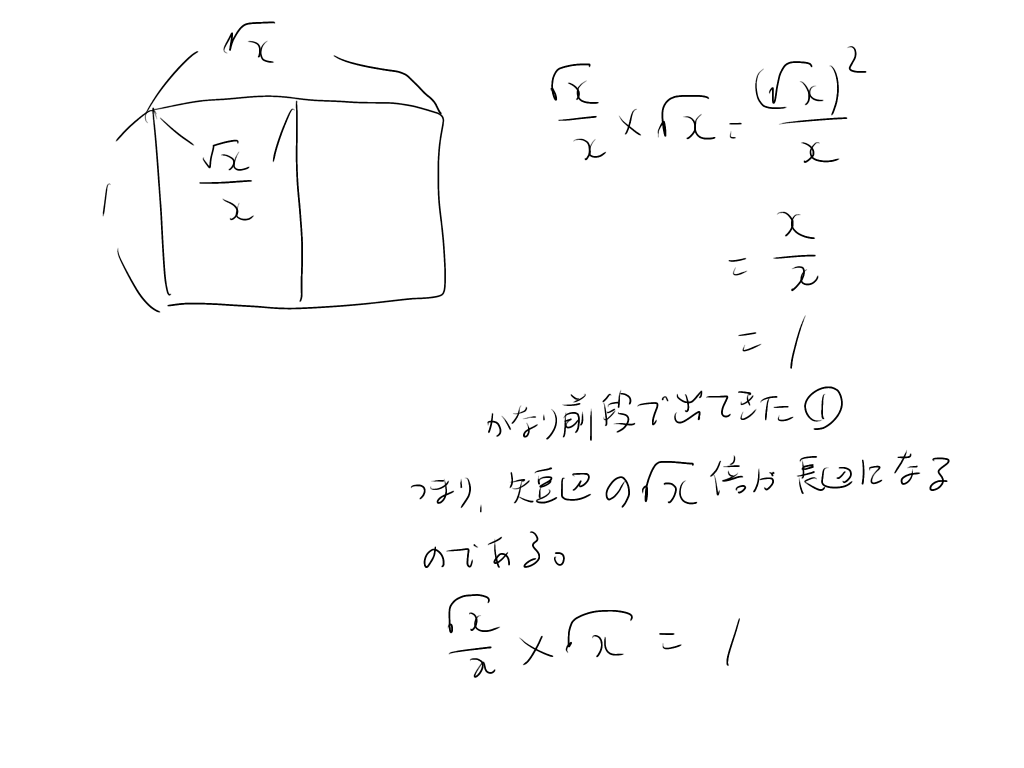
これが証明となる。
この証明を解く鍵は、2等分とかにこだわらず、√の中身と、等分する数の一致に気が付けるかという点と、
√X/Xが√Xと同義であることに気づける点かと思う。
そして1にするためには、その逆数を使えば1になることに気付けば、じつは2等分したときの比率を変えたくなければ、元の比率をどう設定しておくのがいいのかを、逆算することができるのである。
以上。

この長さだと、何等分すれば、縦横比率が変わらないか。。。










コメントを残す